Random_genesis
- Scientific worldbuilding
Constructing fictional places has always been one of the main goals in the general field of procedural generation.
However, in most cases, even the generation of entire worlds has just been a necessary step in the creation of some other product. The generation tends therefore to focus on a few aspects that are core to the final product, while many variables are left aside.
The idea is to try and create large territories, where many different variables are scientifcally taken into account: geology, geography, climate, ecology...
Possibly, through the application of some "Guns, Germs and Steel-like" mechanics it will be possible to simulate large scale interactions between humans and the environment, and among humans on a large scale.
Wraparound Noise (Apr 2018)
>Previous Update
Since i'll be working on winds next, i thought it to be necessary to make the map wraparound so that the winds can be consistent.
The map will only be wraparound on the East-West axis. The northern and southern edges of the map will be covered in non traversable icecaps anyway.
Given that, it all boils down to ensuring that the left and right edges of the map are identic, and that no sudden discontinuities occur anywhere along the X axis.
The correct way to do this depends on how the map is generated in the first place. In this case the map is a matrix, produced as a linear combination of matrices of different kinds: matrices representing voronoi tessellations and matrices representing noise. The map is also smoothed repeatedly.
Noise matrices are inherently wraparound: they lack any structure that would produce discontinuities, and can therefore be ignored.
What needs to be adapted is how the voronoi tessellation is generated, and how the smoothing works.
The way I am doing things, the voronoi tessellation is generated by placing a given number of points (the Seed) on the map, giving each of them a height from a noise source, and then running a 1-NN algorithm on all the cells of the matrix. Each pixel gets the value of the nearest point.
In order for this to work across the edges of the map, it is sufficient to change the distance function used, so that the closest point can be searched through the opposite side of the matrix.
On a wraparound map, two points A and B lie on a circle, representing the ideal surface of the planet. The distance between the two becomes then the minimum between the clockwise and counter-clockwise measures.
To measure the flat distance from A to B, it is sufficient to "mirror" B on the closest edge of the map, producing a new point B'. The final distance is the minimum between the one from A to B and that from A to B'.
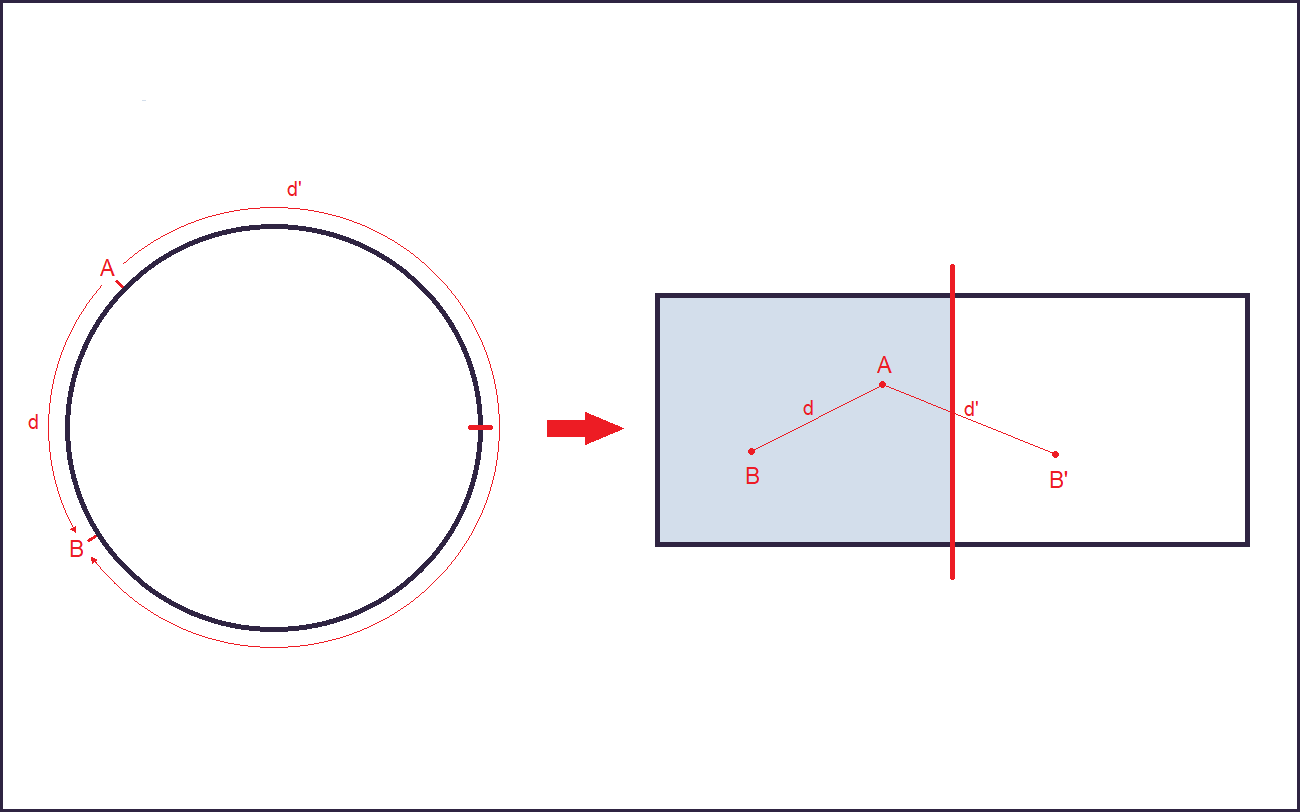
This means that the computations required for the 1-NN algorithm are doubled: two distances need to be calculated for each cell instead of one.
Although this cannot change in absolute terms some optimization can be made.
In order to do this, one can reason on the geometry of the problem to reduce the cases in which the second distance d(A,B') is needed.
In fact, if the "standard" distance d(A,B) is smaller than the distance between A and the closest edge of the map, d(A,B') will invariably be larger than d(A,B), and therefore can be ignored alltogether.
This is because B' is on the other side of the edge by definition, so in order to get from A to B' one would need to get to the edge first, and then from there to B'. This means that d(A,B') will always be greater than d(A,Edge).
1-NN requires that we calculate, for every cell A of the matrix:
min(d(A,B),d(A,B')), ∀B∈Seed
Once a B closer than the closest edge to A is found, not only we can forget about the "around-the-world" distance d(A,B') for that specific B, but also we can ignore it for every other point that comes after B in the 1-NN algorithm. This is because we already have a distance that is certainly smaller than the "around-the-world" distance from A to any other point.
It is hard to calculate the exact computational impact of this optimization, as it really depends on the distribution of the seed: a denser seed will certainly make it so that a "close enough" point is found earlier and the number of distances needed per element of the seed falls to 1 earlier. At the same time a denser seed means more points.
In the end the size of the seed (and therefore its density) depends on the geographical features of the map being generated, so it's not really something that can be tweaked to optimize computation times.
The algorithm was tested to obtain an empirical estimate of how frequently the additional distance needs to be calculated: 100 runs, 384+256 cells, 180 points in the seed.
As it turns out, on average, the 1-NN skips the additional distance calculation 88% of the times. Meaning that having a wraparound map instead of a flat one is only 12% more time consuming.
The images below show the map before and after the change in how the voronoi diagram is generated: the map is shifted by 50% along the X axis so that the original edge is in the middle (marked with a red line).
(before)

(after)

The discontinuity along the edge of the map is gone. This means that all voronoi layers used in generating the map will be wraparound.
This is not enough, though. The map generation also employs several passes of smoothing, and that is not wraparound yet. In fact the smoothing is done calculating the mean of the values in a certain radius around a cell, and then assigning the result to the cell.
When the area being smoothed is close to an edge, some of the neighbours that need to be used in calculating the mean will be out of the matrix, and are currently ignored.
This naturally causes the smoothing not to work across the edge of the map. However, fixing this is trivial: when the cell being looked at is out of the boundaries of the matrix, add/subtract the size of the map along the X axis to look at the corresponding cell on the opposite side of the map.
This way, when the smoothing loop is looking at the cell with x value -1, it will look at x value xSize-1 instead. The same holds in the other direction: x value xSize+1 becomes x value +1.
The pictures below show a complete map before and after these changes. Again it is shifted so that it centers on its former edge.
(before)

(after)

Now the map is actually wraparound, and no discontinuity exists along its x axis.
This means that it is actually possible to work on meaningful climate features, notably winds. This would have not been possible before, since winds need to flow uninterrupted around the "planet", and given that they are influenced by land elevation they need a wraparound elevation map.
