Random_genesis
- Scientific worldbuilding
Constructing fictional places has always been one of the main goals in the general field of procedural generation.
However, in most cases, even the generation of entire worlds has just been a necessary step in the creation of some other product. The generation tends therefore to focus on a few aspects that are core to the final product, while many variables are left aside.
The idea is to try and create large territories, where many different variables are scientifcally taken into account: geology, geography, climate, ecology...
Possibly, through the application of some "Guns, Germs and Steel-like" mechanics it will be possible to simulate large scale interactions between humans and the environment, and among humans on a large scale.
Wind Generation (Oct 2018)
>Previous Update
Up until this point, we have a way of generating sensible heighmaps, and a way of distributing sensible temperature values, month by month.
The next step in the construction of a simple climate simulation model is to introduce wind.
Since the aim of this is to generate large scale environments, the focus will be on average, long distance, currents rather than on local phenomena.
The factor which define direction and speed of air currents are several. Since the goal of this work is to produce credible results rather than fully
replicating real world mechanics, the main factor that will be taken into account is heat.
The uneven distribution of heat on the Earth's surface is the main driving factor between what is called "Atmospheric circulation", meaning vast flows of air that
balance the distribution of thermal energy. These flows, called "cells", remain basically unchanged for millions of years, because they depend on relatively constant parameters, such as
the thermal properties of air, the flow of energy from the Sun, the Earth's diamater, and so on.
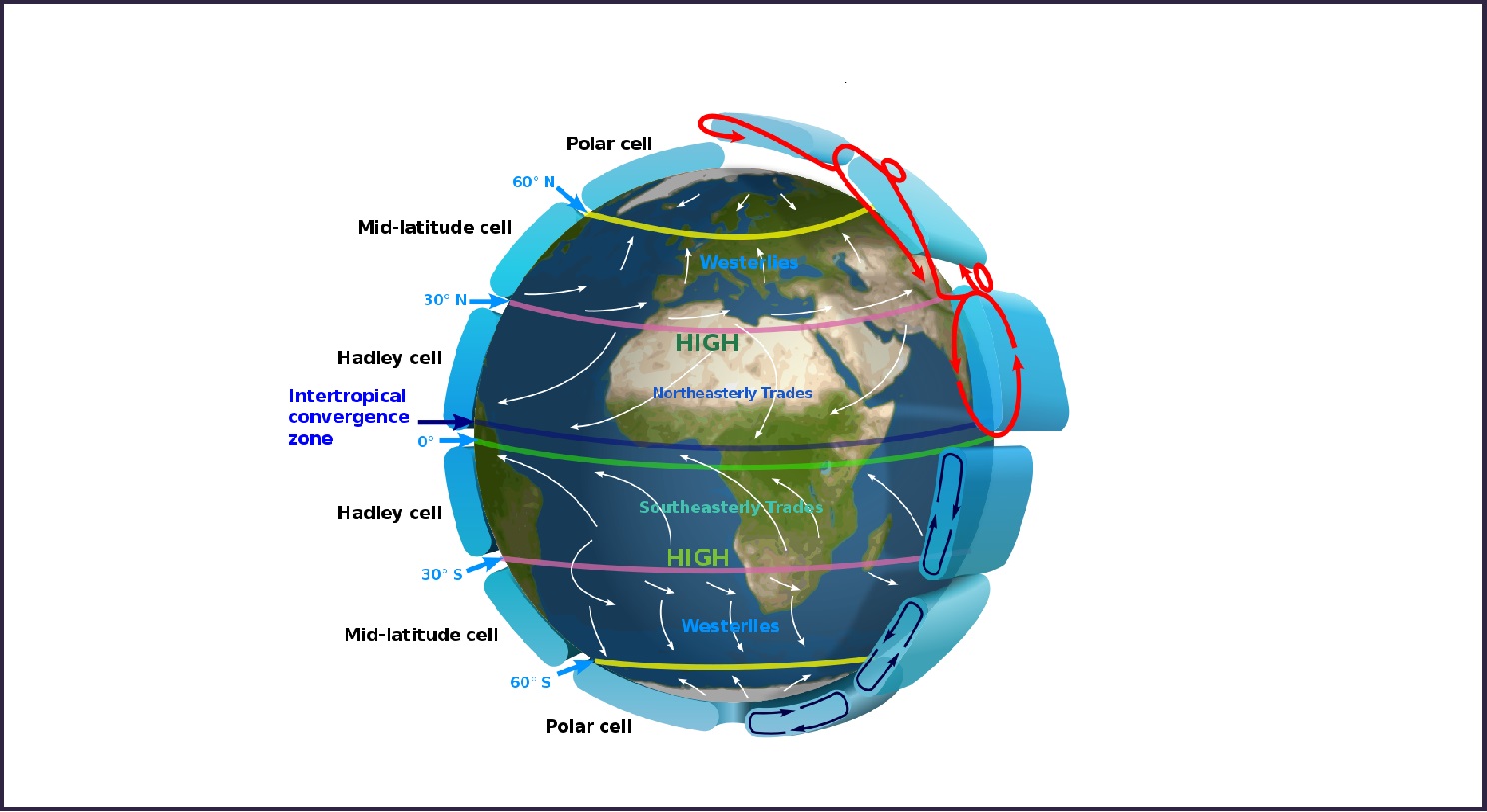
This constant flow of air in a fixed direction, together with the Coriolis effect caused by the rotation of the Earth, causes what are usually called "Prevailing winds", or "Trade winds":
persistent air currents that blow, generally, in the same direction all the time. These winds have been the determining factor behind the emergence of trade routes in the age of sail, and
are a major force in the climate of many coastal regions.
Simulating these winds is quite simple, since there is no need to implement the complex mechanix behind them. Flow direction and flow speed are merely function of the latitude.
Direction was sourced by various description of prevailing winds found on the internet, as well as from images such as the one shown above (from Wikipedia).
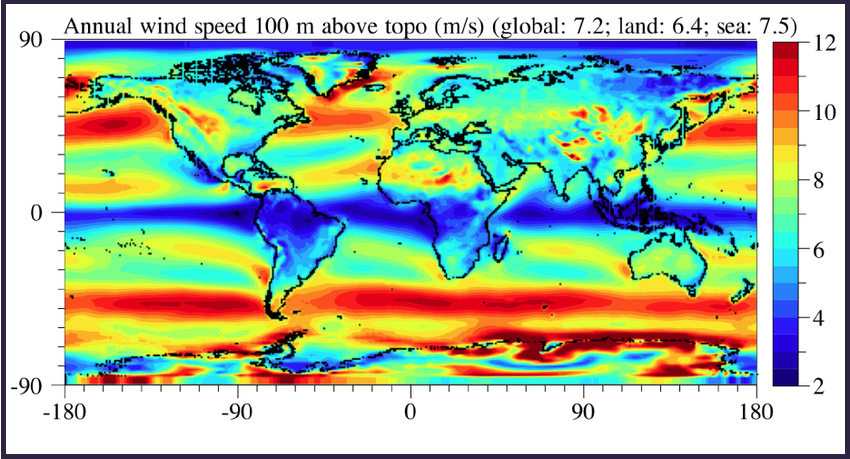
Defining wind speed was a bit more complicated. However once again there are numerous resources online one can start from, presenting numeric data as well as images such as this (researchgate.net):
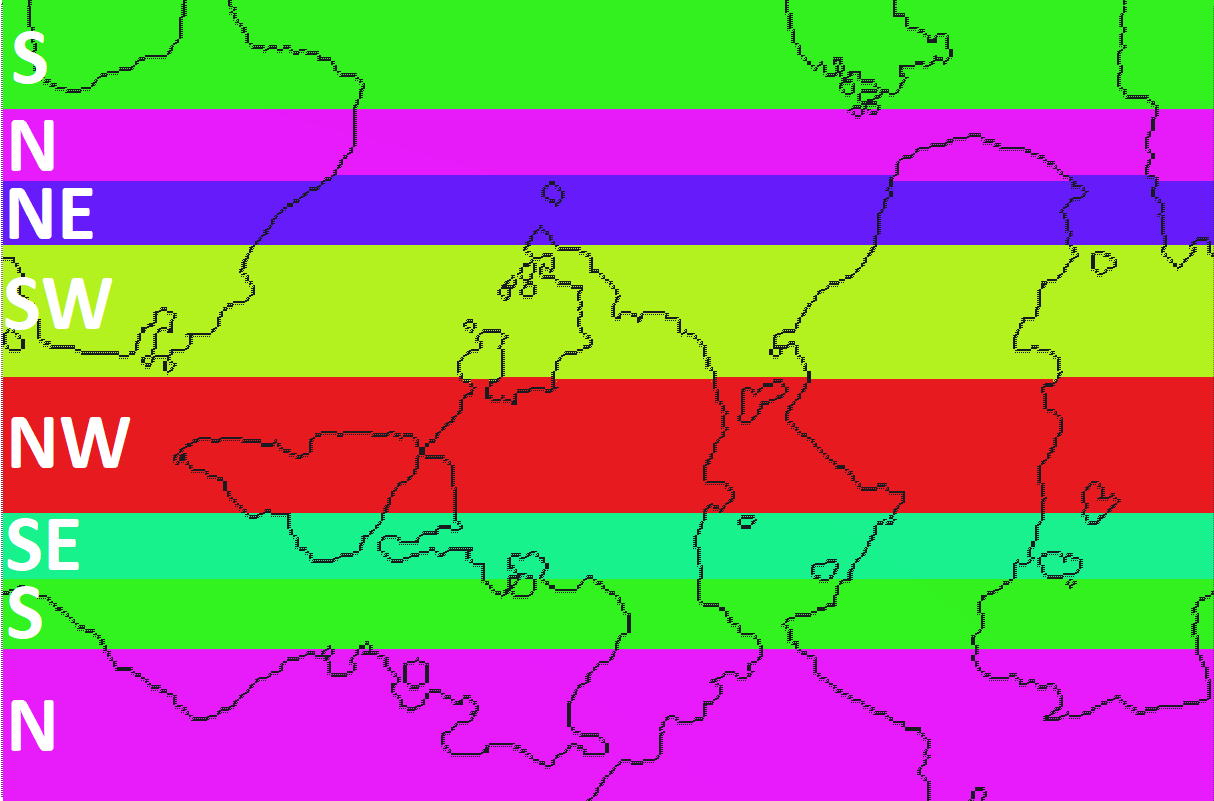
These are the results of the two functions I came up with to sort-of reproduce real world values. On the left a map showing the direction of trade winds, and on the right a map of wind speed.

Clearly, this would only be acceptable if the Earth was a perfectly smooth ball of ocean, but it isn't. An other factor that is going to be considered is the differential of temperature
caused by landmasses and elevation. This causes a difference in pressure, since warmer air tends to rise and displace colder one. In turn this causes a flow at ground height from cold to warmer areas, when the surrounding air
moves towards the lower pressure. There is a symmetric flow of fluid in the opposite direction above, but since only ground level wind is being simulated, this can be ignored.
This was simulated via a recursive algorithm: given a square of size S, the average temperature along its four edges is calculated. The wind then flows from the coldest edge to the warmest,
with a speed proportional to the difference in average temperature between the two.
Starting from S=32, each square is divided into four, and the calculation is performed on them. The final result is a weighted blending of all the squares of all sizes.
Given that smaller squares will usually produce weaker winds, due to the fact that the differential in temperature is smaller, the weighting is done in a way that reinforces smaller squares.
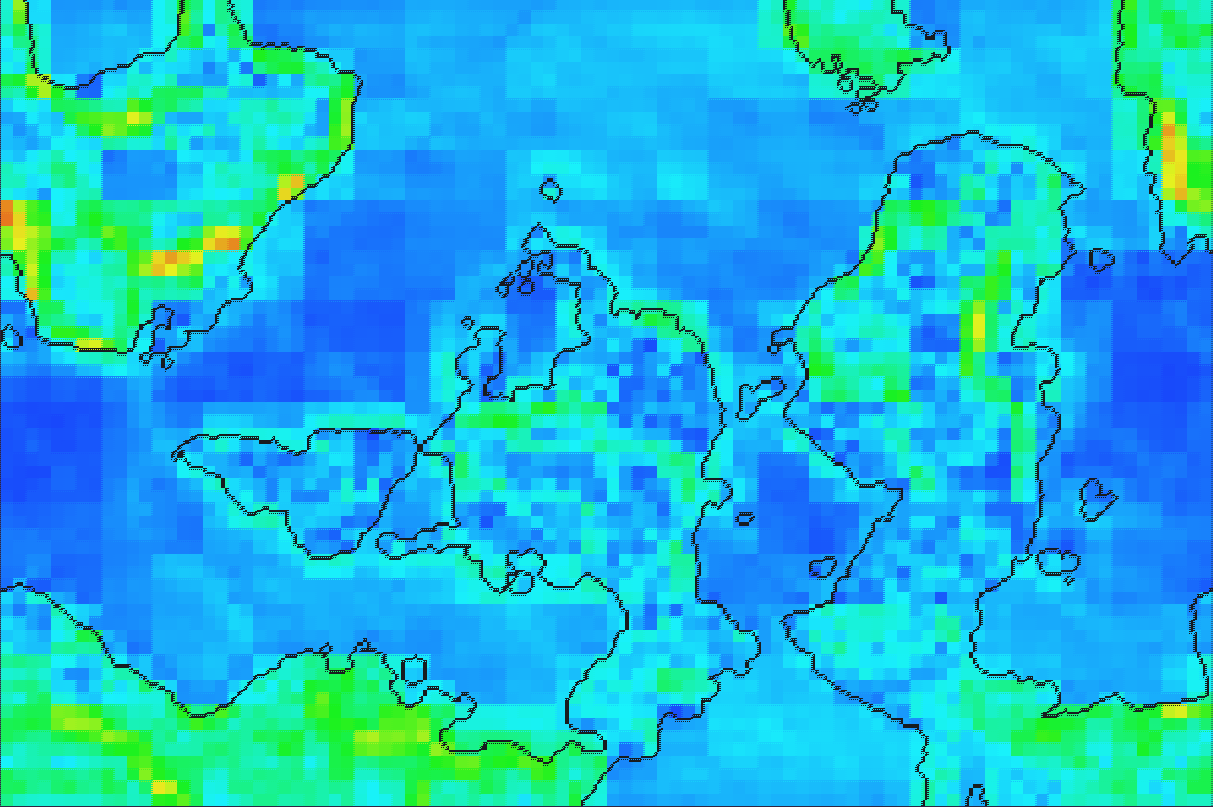
This required some delicate tweaking of the many parameters involved, in the end these are the outputs.
Again, direction on the left and speed on the right

At this point we have two different wind maps: one with "trade winds", and one with winds generated by temperature differential. The two need to be blended together to produce a final global wind map.
A fact must be taken into consideration: trade winds are already a function of differential temperatures (and coriolis effect). If, at any point, one was to sum the two maps, the temperature would contrbute twice to the final output.
Therefore the blending is done via a convex combination of the two map values. The blending parameter itself is defined as a parable, function of altitude.
At sea, the "trade wind" map contributes almost alone to the final value. its weight decreases quickly with altitude, until it goes to zero after a certain point.
After blending the two maps, the final map is smoothed repeatedly, setting each point (a 2D vector) to the average of its neighbours.
Here are the results:

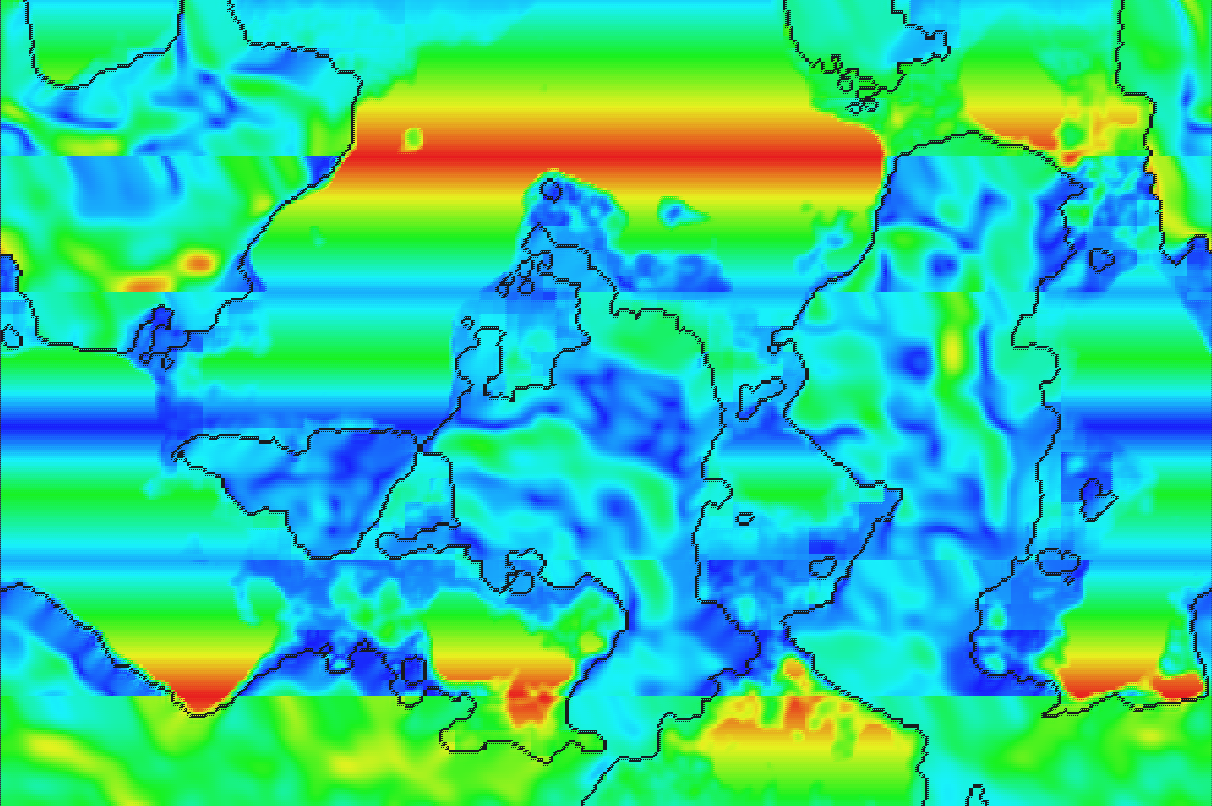
A limit to this approach is the statistical prevalence of winds along the Nort-South axis. This depends on the reliance on a square to calculate the direction of temperature differentials:
since adjacent edges in a square have part of their points closer to one another, their average temperatures are likely to be similar. Edges that are opposite in the square are much more likely
to dominate in temperature differential, especially the (North, South) pair, because of the change in temperature given by latitude.
Changing the algorithm from a square-based approach to a radial one would be very complex. I might return to it at a later date, but for now the output seems natural enoughto be acceptable.
With wind in place, the next logical step is going to be a precipitation model.
