Random_genesis
- "Boggle-like" matrices
Boggle™ is a word game designed in the '70s, in which players try to compose as many words as possible with 16 letters arranged in a 4x4 matrix.
the matrix is "randomly" generated by shaking 16 dice, each having a letter on each of the 6 faces.
Similar games have been ubiquitously marketed under different names, even in digital form.
Given a matrix size and a dictionary of words, there are obviously numerous ways to generate the matrix.
How does one generate it in such a way that it contains the most words?
"Counting words" (Jul 2018)
As a first step it is necessary to code a function that, given a matrix of letters, returns the set of all the words that can be composed with it.
For this, as for the rest of this project, I will be using Python 3.7.
A nxn matrix of letters can be seen as a graph G with n^2 nodes. Two nodes in G are connected with an edge if they are adjacent to each other. Oblique adjacency is valid.
That said, a word can simply be seen as a loopless path on G that belongs to the given dictionary.
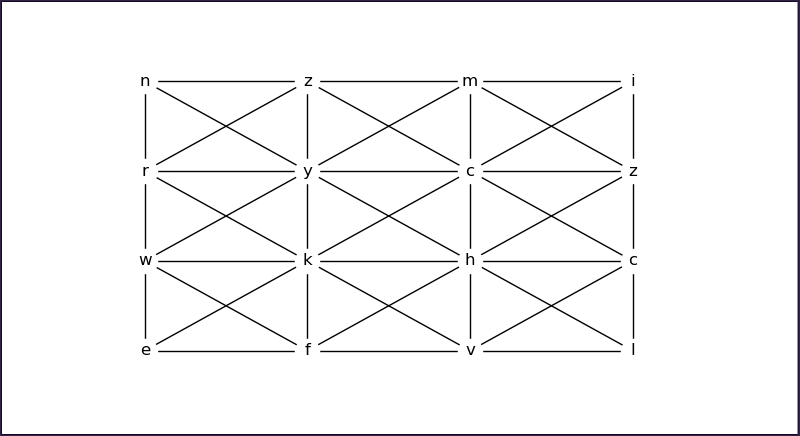
The function can thus iterate on the letters in the matrix,
exploring all the paths originating from each of them, and accumulating every word it encounters, using any graph search strategy.
The problem is that the number of possible paths on a graph is a rather large one.
In this case, since the longest possible word will be 16 letters long, we are looking at paths that cannot be longer than 16. Without calculating the exact number, a rough estimate of the number of paths on G with a length of maximum 16 is something like 16^5, which is an untreatable amount.
It is therefore necessary to design the algorithm so that it recognises a fruitless path as soon as possible, so that it only explores those than could lead to full words.
The algorithm will need to include a data structure capable of responding in constant time to the question "will this path ever lead to any valid word?".
For this I will be using a varant of a prefix tree: a single-parent tree in which nodes can be associated to words, and each of these words is a prefix of all the words associated with nodes downstream.
In most cases prefix trees are designed so that nodes contain full words, in this case single letters are sufficient.
Moreover, each node will be marked with a boolean flag, signalling if it is the terminal letter of a valid word in the dictionary. This is necessary in order to treat the cases in which words of the dicitionary are prefix of each others, such as it is for the terms "hell" and "hello".
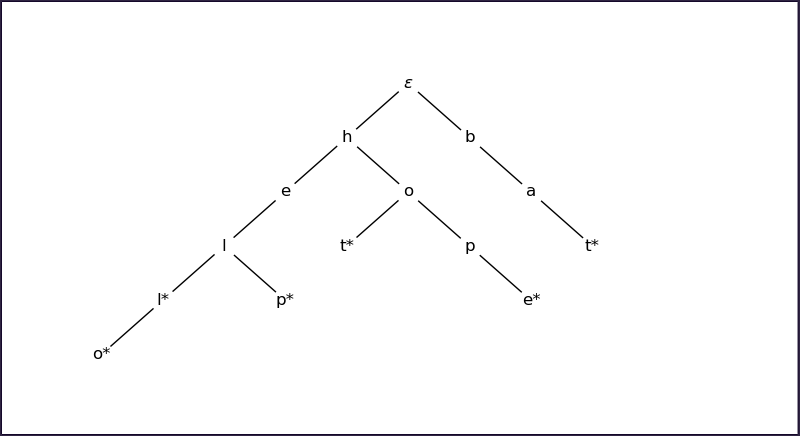
The picture above shows the prefix tree built by the words "hell", "hello", "help", "hot", "hope", and "bat". nodes marked with "*" represent terminal letters.
Building the structure is not a complicated, nor particulary time-hungry process. For each word in the dictionary, starting from the root of the tree (labeled with the empty word "ε"), a branch with maximum length 16 has to be walked/built to ensure that the entire word is stored.
The resulting time complexity is then Θ(n) for a dictionary containing n letters.
Once the structure is in place, given a node in the tree, the question "can this sequence of letters lead to any valid word?" can be answered in Ο(1) time, simply by checking whether the node has any children nodes.
Also, once a node marked as terminal is reached, the corresponding word will be obtainable as the reverse path from the node to the root of the tree.
This data structure will be part of the exploration process. The exploration follows a typical depth-first graph search algorithm, while simultaneously exploring the prefix tree.
Each node in the exploration algorithm contains a reference to the node in the character tree, so that it can be used to stop following that path as soon as it becomes clear that it will lead to no new words.
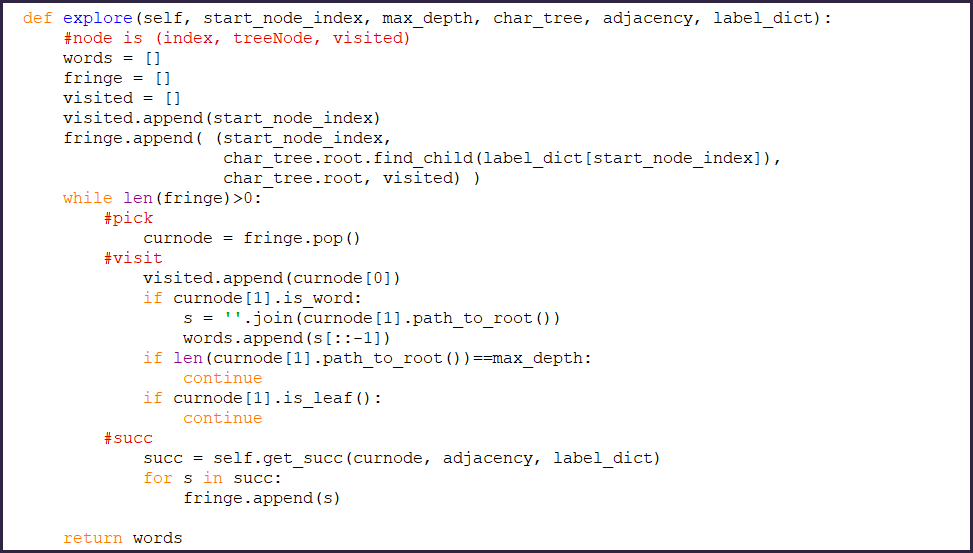
Each item in the exploration queue is a triplet (I,N,V), where I is the matrix cell index, N is a node in the prefix tree, and V is a the set of visited cells. Usually in search algorithms the set of visited nodes is a single global structure shared among all exploration paths.
In this case it needs to be path-specific, since different paths can traverse the same cell (so that different words can use the same letter).
In each iteration, the next item to be visited is picked from the top of the queue, inducing a DF search. Then the corresponding cell is marked as visited for all the exploration paths that cross it.
If the corresponding prefix tree node represents a complete word, said word is added to the output list. If the depth of the current exploration node is at its possible maximum (16, for a 4x4 matrix), the algorithm skips to the next iteration.
Then the prefix tree node is used to determine whether it is useful at all to follow this branch. If it isnt the algorithm skips ahead.
The successor nodes in the path are obtained by intersection of two sets: neighboring unvisited nodes in the graph, and valid characters children of the current prefix tree node. The resuting triplets are added to the exploration queue.
The complete code can be found here.
Iterating on the letters of the matrix, the algorithm will be initialized with the sub-tree belongin to the current letter, and will follow every valid path originating form it.
This simple algorithm can then, given a nxn matrix of letters in input, produce in output the list of all the words that can be found in it, belonging to a given dictionary. The time it takes to do this varies greatly depending on how "good" the matrix is:
matrices that contain many words will take longer to explore, because the algorithm will have to follow numerous valid paths to their end. While "poor" matrices will be explored very quickly, since the algorithm can prune an exploration branch as soon as it reveals to be fruitless.
