Random_genesis
- Islamic architecture
The idea is to hierarchically construct buildings by instantiating pre-modelled, 3D pieces.
A Markov-chain-like grammar can be used to procedurally design a tree of objects, where the leaves are simple solid shapes.
Keeping the models as bare-bone as possible will allow the algorithm to scale in complexity, while simultaneously drastically reducing the costs of the modelling process.
I have chosen to look at islamic architecture for inspiration. I guess it looks more organic and less "planned" than other kinds of monumental art, so that even a randomised group of buildings will look alright.
Not a game, not a complicated algorithm, just a toy.
"Foundations" (Apr 2018)
>Previous update
For now, the complexes I am going for are going to be made of different types of building:
- courtyards surrounded by arches and columns
- non-descriptive, flat-roofed buildings that act as fillers and connections
- square, higher buildings surmounted by domes of various shapes and sizes
- minarets
- "junctions", gates between two buildings.
To procedurally design the general layout of the complex, i am using an algorithm that works similarly to a graph search.
Graph search algorithms mostly follow the same general pattern, while the specific implementation of the primitives and structures involved is what differentiates between them.
The generic graph search uses two data structures that contain sets of nodes: the "visited" set, containing al the nodes already visited by the search, and the "fringe", or "frontier", that holds all those nodes that are known but are yet to be visited.
The generic algorithm goes something like this:
1. Visited is initialised as empty, Fringe is initialised with the initial node
2. while the fringe is not empty, and the search is not finished, repeat
3. select a node N from Fringe
4. remove N from Fringe
5. expand N finding its successors
6. add the successors to Fringe
7. add N to Visited
The algorithm I'm using to distribute buildings around works similarly. However there is no graph involved. Instead of nodes in a graph, my "Fringe" contains "edges": walls of buildings to which an other building can be attached.
Before the actual loop, a total T of buildings is assigned at random, as well as the number of minarets. The algorithm then places down the foundations of a new building at every iteration, until the total is reached, or no usable edges remain.
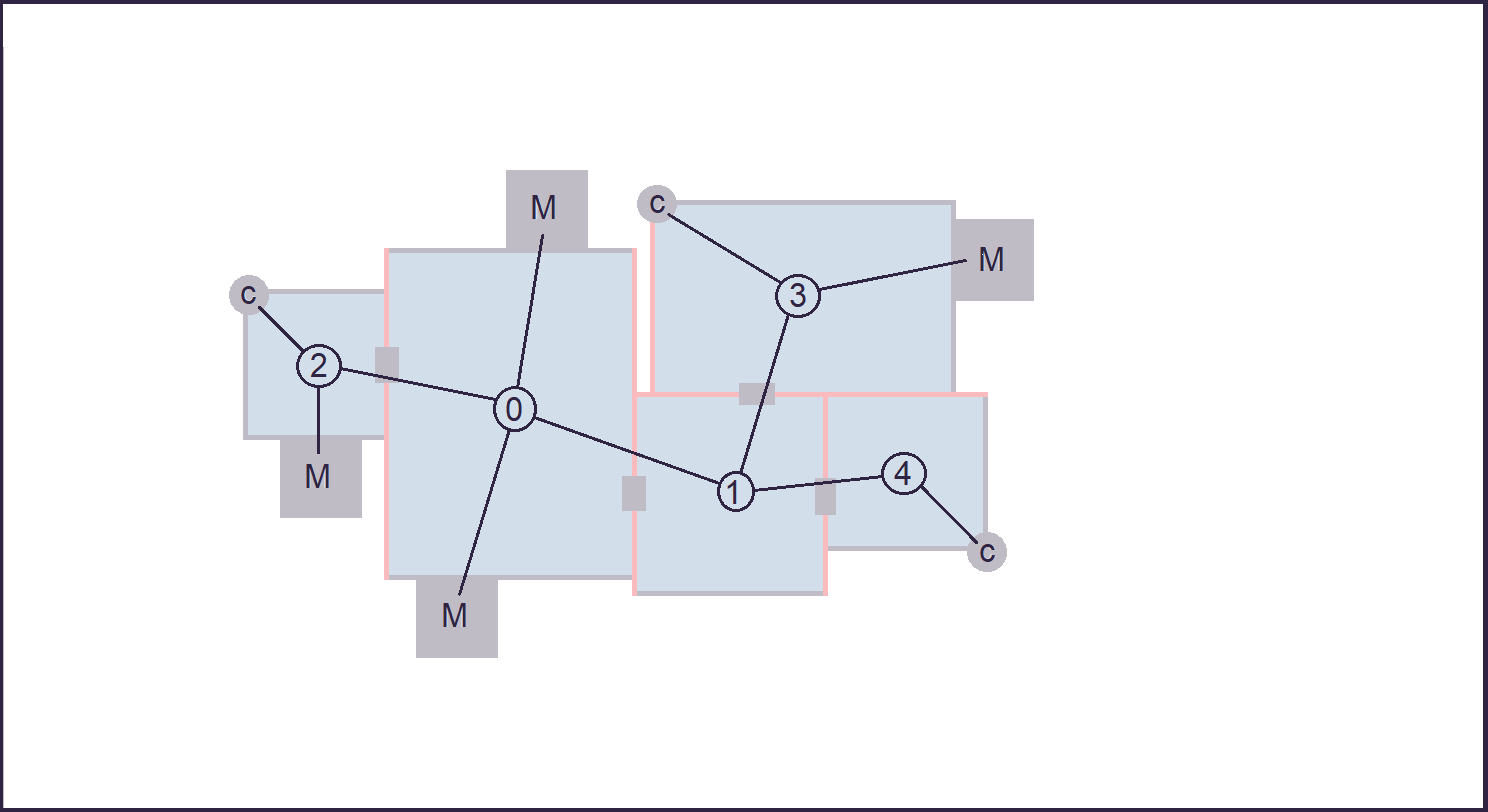
The output of the algorithm is usually in the form of a Directed Acyclic Graph (DAG), representing the nodes encountered/visited/generated.
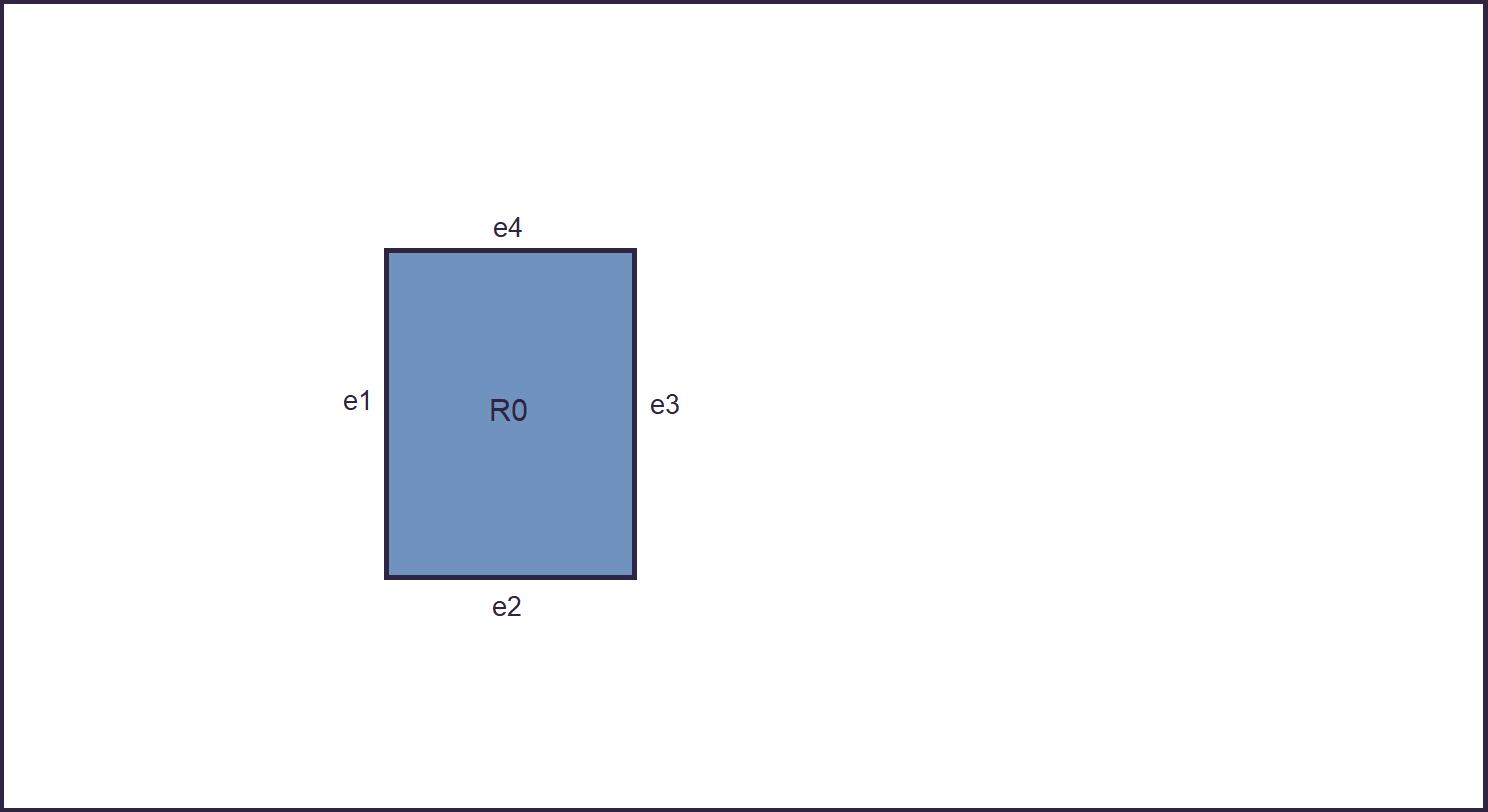
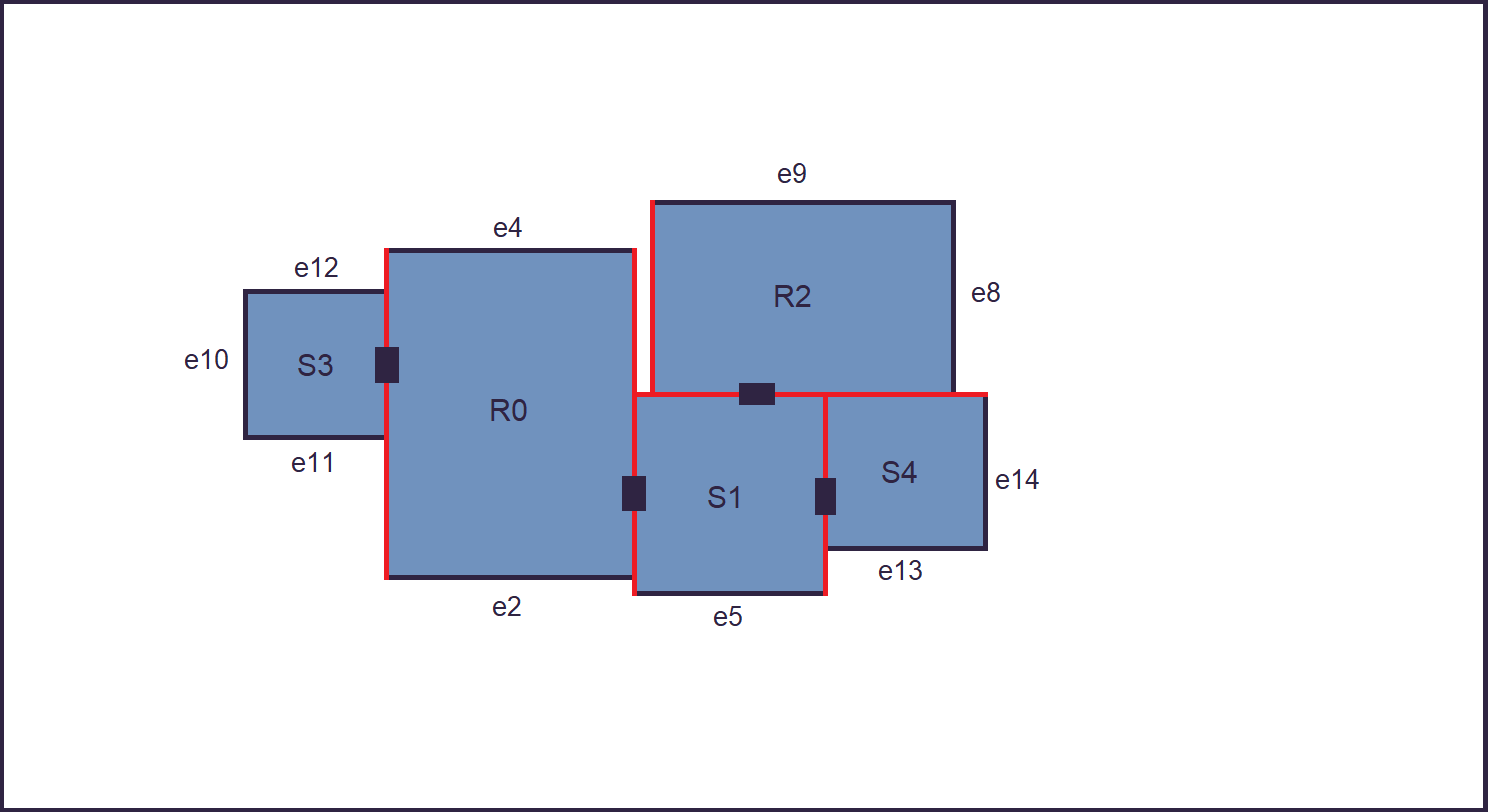
1. A first rectangle is generated. Rectangles are constrained by minimum/maximum side length, and a minimum/maximum ratio between minor and major side. Since they are all usable, its 4 edges are added to the "Edges" set.
Then the main loop.
It iterates until the Fringe set is empty, or until enough buildings have ben placed.
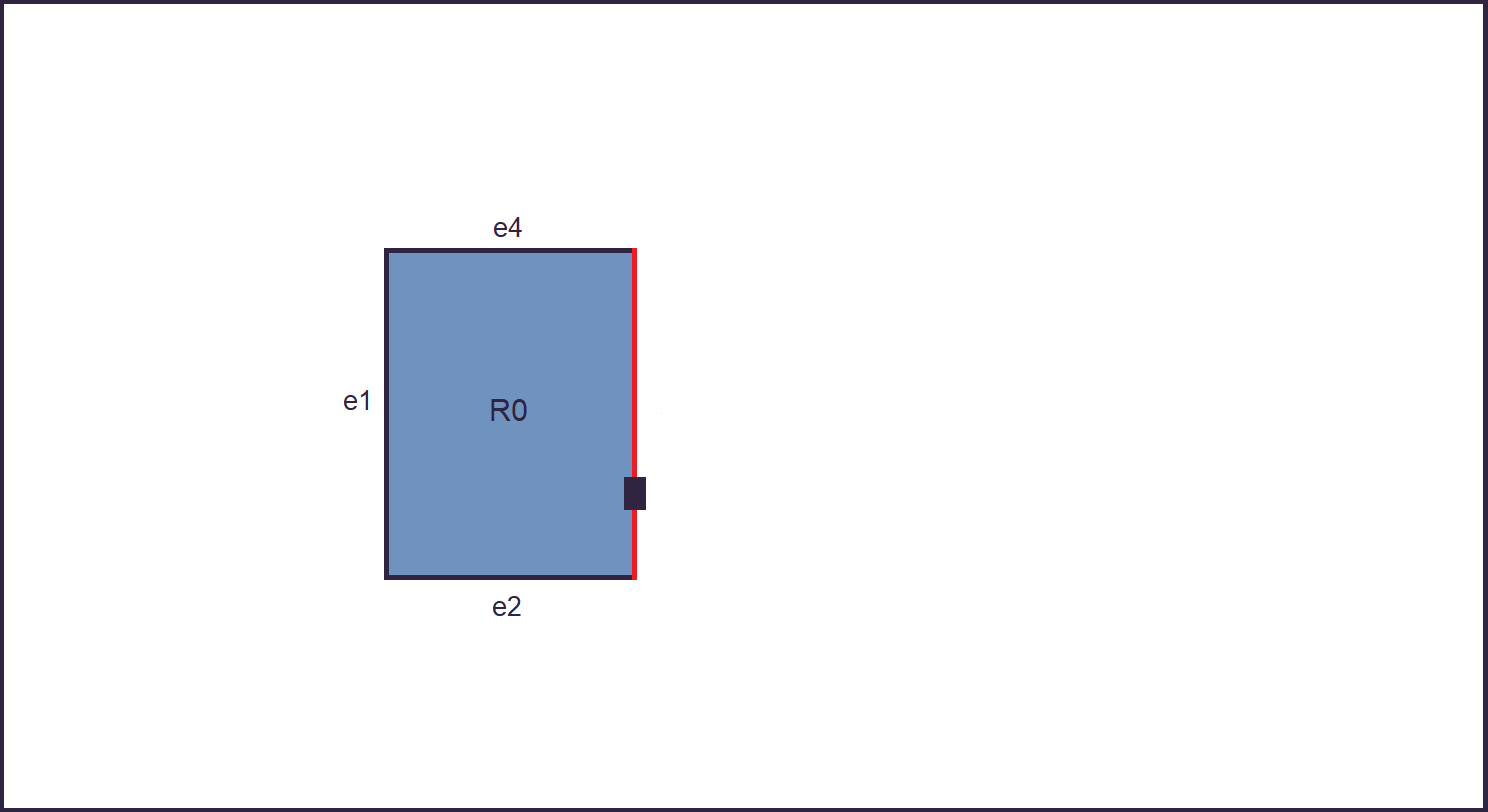
2. An edge is picked at random from the Edges set. A point is randomly selected along it. A junction is placed there.
The edge is removed from the Edges set.
The newly generated junction will be used as a starting point for the generation of a new building.
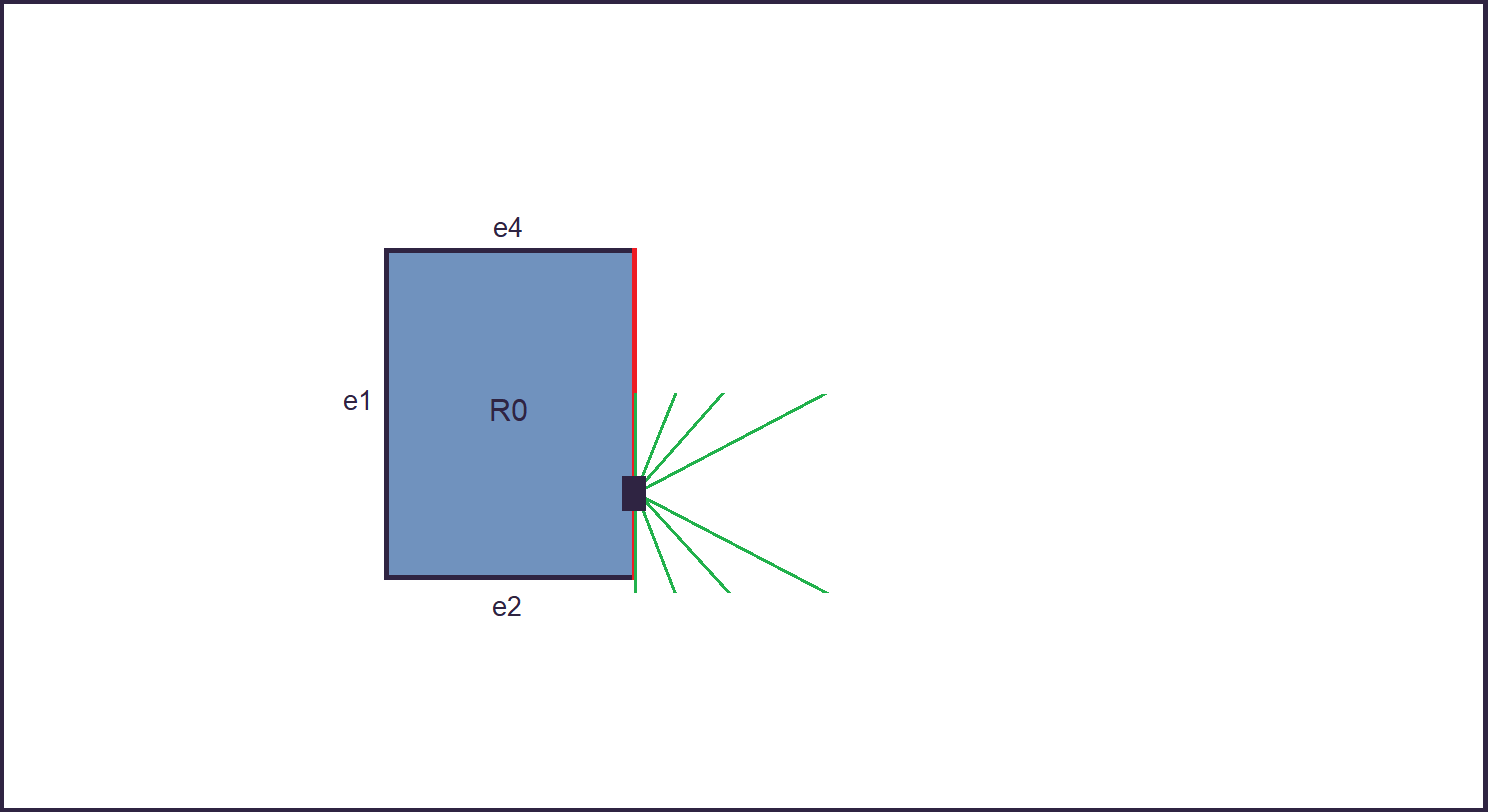
The type of building is selected using a Roulette Selection, where the probability of generating a new rectangle decreases at every iteration.
As a result, while the generation progresses, at first it will be likely to generate rectangles, and then squares.
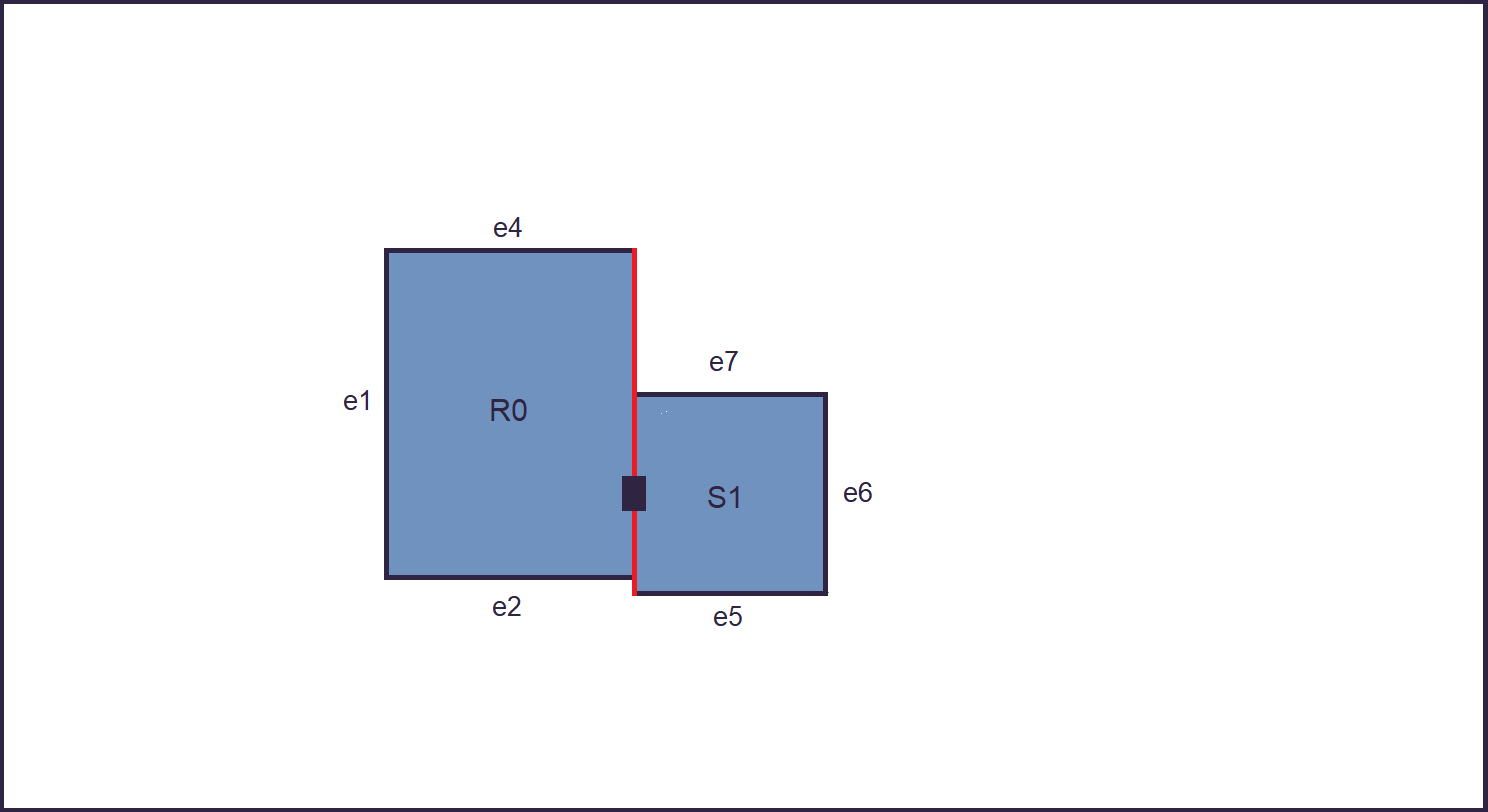
3. Avaliable space is measured from the junction: line of sight from the junction to corners, and line of sight between corners.
Given that there will be no unconnected parts, this is suficient to ensure that a consistent building is generated without overlapping any preexisting one.
If line of sight is broken, this step is attempted again (up to 50 times) with smaller sizes. If no attempts succeed it means that the edge ended up too close to other buildings, and is removed from the set.
4. The new building is placed down, and its edges are added to the pool, excluding the edge use to generate it.
5. As the loop (steps 2 to 4) keeps iterating, more rectangular and square buildings are placed down without overlaps.
The algorithm stops when enough buildings have been laid down. It would also stop if no avaliable edges remained, but that is mathematically impossible and will never happen.
This can be easily proven by induction. However, such demonstration is not within the scope of this page.
6. As a last step, a certain number of smaller squares (that will later become minarets) are added to avaliable edges,
completing the layout of the complex.
Also, the corners of buildings with sufficient space around them are stored in an additional structure.
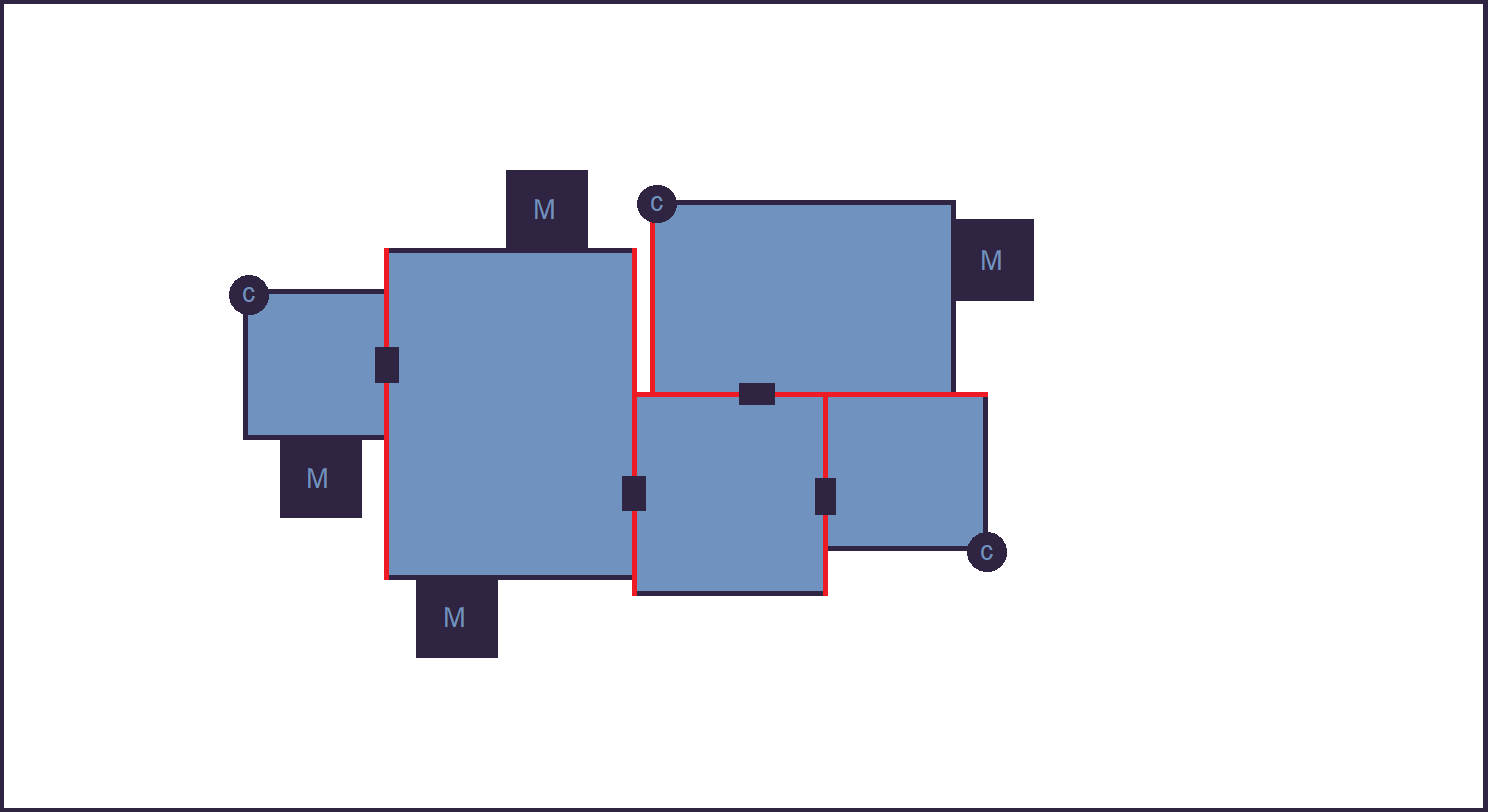
The output given by the algorithm is the description of the layout generated, in the form of:
- A set of "building foundations" (defined by center, corners and type),
- A set of junctions between buildings (defined by position and adjacent buildings),
- A set of free corners.
In the future, each one of these will launch its own algorithm to generate the relative 3D structure.
Returning to the parallel with graph search algorithms, the connections between buildings do in fact describe a DAG (more specifically, a tree).
 >Next update
>Next update
